Homework 3: Supervised Learning Algorithms
Due date: Monday, March 20, 2023 at 11:55pm
Turn in a PDF submission. You may include photos of handwritten solutions within your PDF, but make sure it is legible. Points will be taken off for illegible solutions. Full credit on non-coding problems will only be assigned if your work is shown.
Question 1: Regularization (1 point)
Recall that \(\lambda\) is a regularization parameter which defines regularization strength. You have trained a logistic regression model two times, once with \(\lambda=0\) and once with \(\lambda=1\).The first time, your model learned the following parameters:
\[[0.42, 2.85, 11.21]\]The second time, your model learned the following parameters:
\[[98.22, -42.11, 12.92]\]You forgot which run corresponded to \(\lambda=0\) and \(\lambda=1\).
Did the first run likely correspond to \(\lambda=0\) or \(\lambda=1\)? Why or why not?
Question 2: K-Nearest Neighbors (1 point)
Recall that in a K-Nearest Neighbors (KNN) classifier, k represents the number of nearest neighbors to consider when making a classification decision.
Consider the following training data.
| Input 1: \(x_1\) | Input 2: \(x_2\) | Output: \(y\) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 5 | 1 |
| 0 | 10 | 0 |
| 5 | 0 | 1 |
| 5 | 5 | 1 |
| 5 | 10 | 0 |
| 10 | 0 | 0 |
| 10 | 5 | 0 |
| 10 | 10 | 0 |
(a) What is the classification of point (6, 6) when k=1? Show your work. (0.5 points)
(b) What is the classification of point (6, 6) when k=3? Show your work. (0.5 points)
Question 3: Decision Trees (2 points)
Construct a minimal decision tree which predicts whether a self-driving airplane will crash if it starts its landing procedures given a set of information that it has available. Use information gain. Show your work and calculations for the entire decision tree construction process.
| Foggy? | Excess Gasoline? | Runway Too Close? | Plane Too High? | Crash? |
|---|---|---|---|---|
| yes | yes | no | yes | yes |
| yes | yes | yes | no | yes |
| no | no | yes | no | yes |
| no | yes | no | yes | no |
| yes | no | yes | yes | yes |
| no | yes | yes | yes | no |
Question 4: Support Vector Machines (1 point)
What is the equation of the line describing the decision boundary for a hard margin SVM trained on the following dataset?
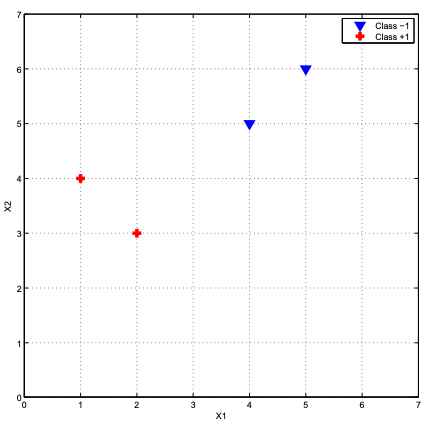
Question 5: Naive Bayes implementation (5 points)
In this problem, you will code a Naive Bayes classifier in Python. Complete the code by filling in the requested probabilities. You can test your code by running the provided example and ensuring that your code’s output matches the expected output.
You may not import any Python library apart from the imports which are already provided in the notebook. This includes sub-libraries (i.e., you cannot use sklearn beyond the svm module used in the helper functions).
Be sure to use Laplacian smoothing for only the conditional probabilities.
Create a copy of this Colab notebook. Submit a publicly accessible link to your notebook copy for this problem in your submitted homework PDF.
Submission instructions
Submit a PDF on Laulima. All of your code must be included in your submitted PDF.